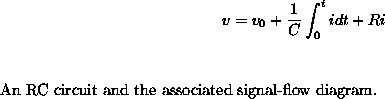Exploiting the Stream Paradigm

SICP > Modularity, Objects, and State > Streams > Exploiting the Stream Paradigm

Streams with delayed evaluation can be a powerful modeling tool, providing many of the benefits of local state and assignment. Moreover, they avoid some of the theoretical tangles that accompany the introduction of assignment into a programming language.
The stream approach can be illuminating because it allows us to build systems with different module boundaries than systems organized around assignment to state variables. For example, we can think of an entire time series (or signal) as a focus of interest, rather than the values of the state variables at individual moments. This makes it convenient to combine and compare components of state from different moments.
Formulating iterations as stream processes
In section , we introduced iterative processes, which proceed by updating state variables. We know now that we can represent state as a ``timeless'' stream of values rather than as a set of variables to be updated. Let's adopt this perspective in revisiting the square-root procedure from section . Recall that the idea is to generate a sequence of better and better guesses for the square root of x by applying over and over again the procedure that improves guesses:
(define (sqrt-improve guess x)
  (average guess (/ x guess)))
In our original sqrt procedure, we made these guesses be the successive values of a state variable. Instead we can generate the infinite stream of guesses, starting with an initial guess of 1:
(define (sqrt-stream x)
  (define guesses
    (cons-stream 1.0
                 (stream-map (lambda (guess)
                               (sqrt-improve guess x))
                             guesses)))
  guesses)

(display-stream (sqrt-stream 2))
1.
1.5
1.4166666666666665
1.4142156862745097
1.4142135623746899
...
We can generate more and more terms of the stream to get better and better guesses. If we like, we can write a procedure that keeps generating terms until the answer is good enough. (See exercise .)
Another iteration that we can treat in the same way is to generate an approximation to $\pi$ , based upon the alternating series that we saw in section :

$\begin{displaymath}\frac {\pi}{4} = 1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots \end{displaymath}$

We first generate the stream of summands of the series (the reciprocals of the odd integers, with alternating signs). Then we take the stream of sums of more and more terms (using the partial-sums procedure of exercise ) and scale the result by 4:
(define (pi-summands n)
  (cons-stream (/ 1.0 n)
               (stream-map - (pi-summands (+ n 2)))))

(define pi-stream
  (scale-stream (partial-sums (pi-summands 1)) 4))

(display-stream pi-stream)
4.
2.666666666666667
3.466666666666667
2.8952380952380956
3.3396825396825403
2.9760461760461765
3.2837384837384844
3.017071817071818
...
This gives us a stream of better and better approximations to , although the approximations converge rather slowly. Eight terms of the sequence bound the value of between 3.284 and 3.017.
So far, our use of the stream of states approach is not much different from updating state variables. But streams give us an opportunity to do some interesting tricks. For example, we can transform a stream with a sequence accelerator that converts a sequence of approximations to a new sequence that converges to the same value as the original, only faster.
One such accelerator, due to the eighteenth-century Swiss mathematician Leonhard Euler, works well with sequences that are partial sums of alternating series (series of terms with alternating signs). In Euler's technique, if S_n is the nth term of the original sum sequence, then the accelerated sequence has terms

$\begin{displaymath}S_{n+1} - \frac{(S_{n+1}-S_n)^2}{S_{n-1}-2S_n+S_{n+1}} \end{displaymath}$

Thus, if the original sequence is represented as a stream of values, the transformed sequence is given by
(define (euler-transform s)
  (let ((s0 (stream-ref s 0))           ; S_n-1
        (s1 (stream-ref s 1))           ; S_n
        (s2 (stream-ref s 2)))          ; S_n+1
    (cons-stream (- s2 (/ (square (- s2 s1))
                          (+ s0 (* -2 s1) s2)))
                 (euler-transform (stream-cdr s)))))
We can demonstrate Euler acceleration with our sequence of approximations to $\pi$ :
(display-stream (euler-transform pi-stream))
3.166666666666667
3.1333333333333337
3.1452380952380956
3.13968253968254
3.1427128427128435
3.1408813408813416
3.142071817071818
3.1412548236077655
...
Even better, we can accelerate the accelerated sequence, and recursively accelerate that, and so on. Namely, we create a stream of streams (a structure we'll call a tableau) in which each stream is the transform of the preceding one:
(define (make-tableau transform s)
  (cons-stream s
               (make-tableau transform
                             (transform s))))
The tableau has the form

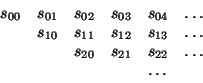
$\begin{displaymath}\begin{array}{llllll} s_{00} & s_{01} & s_{02} & s_{03} & s_{... ...20} & s_{21} & s_{22} & \ldots\cr & & & & \ldots & \end{array}\end{displaymath}$

Finally, we form a sequence by taking the first term in each row of the tableau:
(define (accelerated-sequence transform s)
  (stream-map stream-car
              (make-tableau transform s)))
We can demonstrate this kind of ``super-acceleration'' of the $\pi$ sequence:
(display-stream (accelerated-sequence euler-transform
                                      pi-stream))
4.
3.166666666666667
3.142105263157895
3.141599357319005
3.1415927140337785
3.1415926539752927
3.1415926535911765
3.141592653589778
...
The result is impressive. Taking eight terms of the sequence yields the correct value of to 14 decimal places. If we had used only the original sequence, we would need to compute on the order of 10¹³ terms (i.e., expanding the series far enough so that the individual terms are less then 10^-13) to get that much accuracy!
We could have implemented these acceleration techniques without using streams. But the stream formulation is particularly elegant and convenient because the entire sequence of states is available to us as a data structure that can be manipulated with a uniform set of operations.
Exercise. Louis Reasoner asks why the sqrt-stream procedure was not written in the following more straightforward way, without the local variable guesses:
(define (sqrt-stream x)
  (cons-stream 1.0
               (stream-map (lambda (guess)
                             (sqrt-improve guess x))
                           (sqrt-stream x))))
Alyssa P. Hacker replies that this version of the procedure is considerably less efficient because it performs redundant computation. Explain Alyssa's answer. Would the two versions still differ in efficiency if our implementation of delay used only (lambda () exp) without using the optimization provided by memo-proc (section )?
Exercise. Write a procedure stream-limit that takes as arguments a stream and a number (the tolerance). It should examine the stream until it finds two successive elements that differ in absolute value by less than the tolerance, and return the second of the two elements. Using this, we could compute square roots up to a given tolerance by
(define (sqrt x tolerance)
  (stream-limit (sqrt-stream x) tolerance))
Exercise. Use the series

$\begin{displaymath}\ln 2 = 1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots \end{displaymath}$

to compute three sequences of approximations to the natural logarithm of 2, in the same way we did above for . How rapidly do these sequences converge?
Infinite streams of pairs
In section , we saw how the sequence paradigm handles traditional nested loops as processes defined on sequences of pairs. If we generalize this technique to infinite streams, then we can write programs that are not easily represented as loops, because the ``looping'' must range over an infinite set.
For example, suppose we want to generalize the prime-sum-pairs procedure of section to produce the stream of pairs of all integers (i,j) with $i \leq j$ such that i+j is prime. If int-pairs is the sequence of all pairs of integers (i,j) with $i \leq j$ , then our required stream is simply
(stream-filter (lambda (pair)
                 (prime? (+ (car pair) (cadr pair))))
               int-pairs)
Our problem, then, is to produce the stream int-pairs. More generally, suppose we have two streams S = (S_i) and T = (T_j), and imagine the infinite rectangular array

$\begin{displaymath}\begin{array}{cccc} (S_0,T_0) & (S_0,T_1) & (S_0, T_2) & \ldo... ..._2,T_0) & (S_2,T_1) & (S_2, T_2) & \ldots\cr \ldots \end{array}\end{displaymath}$

We wish to generate a stream that contains all the pairs in the array that lie on or above the diagonal, i.e., the pairs

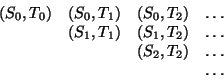
$\begin{displaymath}\begin{array}{cccc} (S_0,T_0) & (S_0,T_1) & (S_0, T_2) & \ldo... ...\ldots\cr & & (S_2, T_2) & \ldots\cr & & & \ldots \end{array}\end{displaymath}$

(If we take both S and T to be the stream of integers, then this will be our desired stream int-pairs.)
Call the general stream of pairs (pairs S T), and consider it to be composed of three parts: the pair (S₀,T₀), the rest of the pairs in the first row, and the remaining pairs:

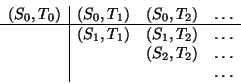
$\begin{displaymath}\begin{array}{c\vert ccc} (S_0,T_0) & (S_0,T_1) & (S_0, T_2) ... ...\ldots\cr & & (S_2, T_2) & \ldots\cr & & & \ldots \end{array}\end{displaymath}$

Observe that the third piece in this decomposition (pairs that are not in the first row) is (recursively) the pairs formed from (stream-cdr S) and (stream-cdr T). Also note that the second piece (the rest of the first row) is
(stream-map (lambda (x) (list (stream-car s) x))
            (stream-cdr t))
Thus we can form our stream of pairs as follows:
(define (pairs s t)
  (cons-stream
   (list (stream-car s) (stream-car t))
   (combine-in-some-way
       (stream-map (lambda (x) (list (stream-car s) x))
                   (stream-cdr t))
       (pairs (stream-cdr s) (stream-cdr t)))))
In order to complete the procedure, we must choose some way to combine the two inner streams. One idea is to use the stream analog of the append procedure from section :
(define (stream-append s1 s2)
  (if (stream-null? s1)
      s2
      (cons-stream (stream-car s1)
                   (stream-append (stream-cdr s1) s2))))
This is unsuitable for infinite streams, however, because it takes all the elements from the first stream before incorporating the second stream. In particular, if we try to generate all pairs of positive integers using
(pairs integers integers)
our stream of results will first try to run through all pairs with the first integer equal to 1, and hence will never produce pairs with any other value of the first integer.
To handle infinite streams, we need to devise an order of combination that ensures that every element will eventually be reached if we let our program run long enough. An elegant way to accomplish this is with the following interleave procedure:
(define (interleave s1 s2)
  (if (stream-null? s1)
      s2
      (cons-stream (stream-car s1)
                   (interleave s2 (stream-cdr s1)))))
Since interleave takes elements alternately from the two streams, every element of the second stream will eventually find its way into the interleaved stream, even if the first stream is infinite.
We can thus generate the required stream of pairs as
(define (pairs s t)
  (cons-stream
   (list (stream-car s) (stream-car t))
   (interleave
    (stream-map (lambda (x) (list (stream-car s) x))
                (stream-cdr t))
    (pairs (stream-cdr s) (stream-cdr t)))))
Exercise. Examine the stream (pairs integers integers). Can you make any general comments about the order in which the pairs are placed into the stream? For example, about how many pairs precede the pair (1,100)? the pair (99,100)? the pair (100,100)? (If you can make precise mathematical statements here, all the better. But feel free to give more qualitative answers if you find yourself getting bogged down.)
Exercise. Modify the pairs procedure so that (pairs integers integers) will produce the stream of all pairs of integers (i,j) (without the condition $i \leq j$ ). Hint: You will need to mix in an additional stream.
Exercise. Louis Reasoner thinks that building a stream of pairs from three parts is unnecessarily complicated. Instead of separating the pair (S₀,T₀) from the rest of the pairs in the first row, he proposes to work with the whole first row, as follows:
(define (pairs s t)
  (interleave
   (stream-map (lambda (x) (list (stream-car s) x))
               t)
   (pairs (stream-cdr s) (stream-cdr t))))
Does this work? Consider what happens if we evaluate (pairs integers integers) using Louis's definition of pairs.
Exercise. Write a procedure triples that takes three infinite streams, S, T, and U, and produces the stream of triples (S_i,T_j,U_k) such that $i \leq j \leq k$ . Use triples to generate the stream of all Pythagorean triples of positive integers, i.e., the triples (i,j,k) such that $i \leq j$ and i² + j² =k².
Exercise. It would be nice to be able to generate streams in which the pairs appear in some useful order, rather than in the order that results from an ad hoc interleaving process. We can use a technique similar to the merge procedure of exercise , if we define a way to say that one pair of integers is ``less than'' another. One way to do this is to define a ``weighting function'' W(i,j) and stipulate that (i₁,j₁) is less than (i₂,j₂) if W(i₁,j₁) < W(i₂,j₂). Write a procedure merge-weighted that is like merge, except that merge-weighted takes an additional argument weight, which is a procedure that computes the weight of a pair, and is used to determine the order in which elements should appear in the resulting merged stream. Using this, generalize pairs to a procedure weighted-pairs that takes two streams, together with a procedure that computes a weighting function, and generates the stream of pairs, ordered according to weight. Use your procedure to generate

a. the stream of all pairs of positive integers (i,j) with $i \leq j$ ordered according to the sum i + j

b. the stream of all pairs of positive integers (i,j) with $i \leq j$ , where neither i nor j is divisible by 2, 3, or 5, and the pairs are ordered according to the sum 2 i + 3 j + 5 i j.
Exercise. Numbers that can be expressed as the sum of two cubes in more than one way are sometimes called Ramanujan numbers, in honor of the mathematician Srinivasa Ramanujan. Ordered streams of pairs provide an elegant solution to the problem of computing these numbers. To find a number that can be written as the sum of two cubes in two different ways, we need only generate the stream of pairs of integers (i,j) weighted according to the sum i³ + j³ (see exercise ), then search the stream for two consecutive pairs with the same weight. Write a procedure to generate the Ramanujan numbers. The first such number is 1,729. What are the next five?
Exercise. In a similar way to exercise generate a stream of all numbers that can be written as the sum of two squares in three different ways (showing how they can be so written).
Streams as signals
We began our discussion of streams by describing them as computational analogs of the ``signals'' in signal-processing systems. In fact, we can use streams to model signal-processing systems in a very direct way, representing the values of a signal at successive time intervals as consecutive elements of a stream. For instance, we can implement an integrator or summer that, for an input stream x=(x_i), an initial value C, and a small increment dt, accumulates the sum

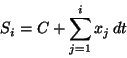
$\begin{displaymath}S_i =C +\sum_{j=1}^{i} x_{j} \, dt \end{displaymath}$

and returns the stream of values S=(S_i). The following integral procedure is reminiscent of the ``implicit style'' definition of the stream of integers (section ):
(define (integral integrand initial-value dt)
  (define int
    (cons-stream initial-value
                 (add-streams (scale-stream integrand dt)
                              int)))
  int)
$\begin{figure}\par\figcaption {The {\tt integral} procedure viewed as a signal-processing system.}\end{figure}$

Figure is a picture of a signal-processing system that corresponds to the integral procedure. The input stream is scaled by dt and passed through an adder, whose output is passed back through the same adder. The self-reference in the definition of int is reflected in the figure by the feedback loop that connects the output of the adder to one of the inputs.
Exercise.

$\begin{figure}\centerline {\hbox{ } \hskip 30pt \vbox{ \hbox {${\displaystyl... ...r\figcaption {An RC circuit and the associated signal-flow diagram.}\end{figure}$

We can model electrical circuits using streams to represent the values of currents or voltages at a sequence of times. For instance, suppose we have an RC circuit consisting of a resistor of resistance R and a capacitor of capacitance C in series. The voltage response v of the circuit to an injected current i is determined by the formula in figure , whose structure is shown by the accompanying signal-flow diagram.
Write a procedure RC that models this circuit. RC should take as inputs the values of R, C, and dt and should return a procedure that takes as inputs a stream representing the current i and an initial value for the capacitor voltage v₀ and produces as output the stream of voltages v. For example, you should be able to use RC to model an RC circuit with R = 5 ohms, C = 1 farad, and a 0.5-second time step by evaluating (define RC1 (RC 5 1 0.5)). This defines RC1 as a procedure that takes a stream representing the time sequence of currents and an initial capacitor voltage and produces the output stream of voltages.
Exercise. Alyssa P. Hacker is designing a system to process signals coming from physical sensors. One important feature she wishes to produce is a signal that describes the zero crossings of the input signal. That is, the resulting signal should be +1 whenever the input signal changes from negative to positive, -1 whenever the input signal changes from positive to negative, and 0 otherwise. (Assume that the sign of a 0 input is positive.) For example, a typical input signal with its associated zero-crossing signal would be
...1  2  1.5  1  0.5  -0.1  -2  -3  -2  -0.5  0.2  3  4 ...
...0  0    0  0    0     -1  0   0   0     0    1  0  0 ...
In Alyssa's system, the signal from the sensor is represented as a stream sensedata and the stream zero-crossings is the corresponding stream of zero crossings. Alyssa first writes a procedure sign-change-detector that takes two values as arguments and compares the signs of the values to produce an appropriate 0, 1, or -1. She then constructs her zero-crossing stream as follows:
(define (make-zero-crossings input-stream last-value)
  (cons-stream
   (sign-change-detector (stream-car input-stream) last-value)
   (make-zero-crossings (stream-cdr input-stream)
                        (stream-car input-stream))))


(define zero-crossings (make-zero-crossings sense-data 0))
Alyssa's boss, Eva Lu Ator, walks by and suggests that this program is approximately equivalent to the following one, which uses the generalized version of stream-map from exercise :
(define zero-crossings
  (stream-map sign-change-detector sense-data expression))
Complete the program by supplying the indicated expression.
Exercise. Unfortunately, Alyssa's zero-crossing detector in exercise proves to be insufficient, because the noisy signal from the sensor leads to spurious zero crossings. Lem E. Tweakit, a hardware specialist, suggests that Alyssa smooth the signal to filter out the noise before extracting the zero crossings. Alyssa takes his advice and decides to extract the zero crossings from the signal constructed by averaging each value of the sense data with the previous value. She explains the problem to her assistant, Louis Reasoner, who attempts to implement the idea, altering Alyssa's program as follows:
(define (make-zero-crossings input-stream last-value)
  (let ((avpt (/ (+ (stream-car input-stream) last-value) 2)))
    (cons-stream (sign-change-detector avpt last-value)
                 (make-zero-crossings (stream-cdr input-stream)
                                      avpt))))
This does not correctly implement Alyssa's plan. Find the bug that Louis has installed and fix it without changing the structure of the program. (Hint: You will need to increase the number of arguments to make-zero-crossings.)
Exercise. Eva Lu Ator has a criticism of Louis's approach in exercise . The program he wrote is not modular, because it intermixes the operation of smoothing with the zero-crossing extraction. For example, the extractor should not have to be changed if Alyssa finds a better way to condition her input signal. Help Louis by writing a procedure smooth that takes a stream as input and produces a stream in which each element is the average of two successive input stream elements. Then use smooth as a component to implement the zero-crossing detector in a more modular style.

Previous: Infinite Streams

Next: Streams and Delayed Evaluation

webmaster@arsdigita.org