Streams and Delayed Evaluation

SICP > Modularity, Objects, and State > Streams > Streams and Delayed Evaluation

Previous: Exploiting the Stream Paradigm

Next: Modularity of Functional Programs and Modularity of Objects

The integral procedure at the end of the preceding section shows how we can use streams to model signal-processing systems that contain feedback loops. The feedback loop for the adder shown in figure is modeled by the fact that integral's internal stream int is defined in terms of itself:
(define int
  (cons-stream initial-value
               (add-streams (scale-stream integrand dt)
                            int)))
The interpreter's ability to deal with such an implicit definition depends on the delay that is incorporated into cons-stream. Without this delay, the interpreter could not construct int before evaluating both arguments to cons-stream, which would require that int already be defined. In general, delay is crucial for using streams to model signal-processing systems that contain loops. Without delay, our models would have to be formulated so that the inputs to any signal-processing component would be fully evaluated before the output could be produced. This would outlaw loops.
Unfortunately, stream models of systems with loops may require uses of delay beyond the ``hidden'' delay supplied by cons-stream. For instance, figure shows a signal-processing system for solving the differential equation dy/dt=f(y) where f is a given function. The figure shows a mapping component, which applies f to its input signal, linked in a feedback loop to an integrator in a manner very similar to that of the analog computer circuits that are actually used to solve such equations.

$\begin{figure}% latex2html id marker 13950 \par\figcaption {An \lq\lq analog computer circuit'' that solves the equation $dy/dt=f(y)$ .}\end{figure}$

Assuming we are given an initial value y₀ for y, we could try to model this system using the procedure
(define (solve f y0 dt)
  (define y (integral dy y0 dt))
  (define dy (stream-map f y))
  y)
This procedure does not work, because in the first line of solve the call to integral requires that the input dy be defined, which does not happen until the second line of solve.
On the other hand, the intent of our definition does make sense, because we can, in principle, begin to generate the y stream without knowing dy. Indeed, integral and many other stream operations have properties similar to those of cons-stream, in that we can generate part of the answer given only partial information about the arguments. For integral, the first element of the output stream is the specified initialvalue. Thus, we can generate the first element of the output stream without evaluating the integrand dy. Once we know the first element of y, the stream-map in the second line of solve can begin working to generate the first element of dy, which will produce the next element of y, and so on.
To take advantage of this idea, we will redefine integral to expect the integrand stream to be a delayed argument. Integral will force the integrand to be evaluated only when it is required to generate more than the first element of the output stream:
(define (integral delayed-integrand initial-value dt)
  (define int
    (cons-stream initial-value
                 (let ((integrand (force delayed-integrand)))
                   (add-streams (scale-stream integrand dt)
                                int))))
  int)
Now we can implement our solve procedure by delaying the evaluation of dy in the definition of y:
(define (solve f y0 dt)
  (define y (integral (delay dy) y0 dt))
  (define dy (stream-map f y))
  y)
In general, every caller of integral must now delay the integrand argument. We can demonstrate that the solve procedure works by approximating by computing the value at y=1 of the solution to the differential equation dy/dt=y with initial condition y(0)=1:
(stream-ref (solve (lambda (y) y) 1 0.001) 1000)
2.716924
Exercise. The integral procedure used above was analogous to the ``implicit'' definition of the infinite stream of integers in section . Alternatively, we can give a definition of integral that is more like integers-starting-from (also in section ):
(define (integral integrand initial-value dt)
  (cons-stream initial-value
               (if (stream-null? integrand)
                   the-empty-stream
                   (integral (stream-cdr integrand)
                             (+ (* dt (stream-car integrand))
                                initial-value)
                             dt))))
When used in systems with loops, this procedure has the same problem as does our original version of integral. Modify the procedure so that it expects the integrand as a delayed argument and hence can be used in the solve procedure shown above.
Exercise.

$\begin{figure}% latex2html id marker 13990 \par\figcaption {Signal-flow diagram for the solution to a second-order linear differential equation.}\end{figure}$

Consider the problem of designing a signal-processing system to study the homogeneous second-order linear differential equation

$\begin{displaymath}\frac {d^{2} y}{dt^{2}}-a\frac{dy}{dt}-by=0 \end{displaymath}$

The output stream, modeling y, is generated by a network that contains a loop. This is because the value of d²y/dt² depends upon the values of y and dy/dt and both of these are determined by integrating d²y/dt². The diagram we would like to encode is shown in figure . Write a procedure solve-2nd that takes as arguments the constants a, b, and dt and the initial values y₀ and dy₀ for y and dy/dt and generates the stream of successive values of y.
Exercise. Generalize the solve-2nd procedure of exercise so that it can be used to solve general second-order differential equations $d^{2} y/dt^{2}=f(dy/dt,\, y)$ .
Exercise. A series RLC circuit consists of a resistor, a capacitor, and an inductor connected in series, as shown in figure . If R, L, and C are the resistance, inductance, and capacitance, then the relations between voltage (v) and current (i) for the three components are described by the equations

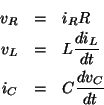
$\begin{eqnarray*}v_{R} &=& i_{R} R\\ v_{L} &=& L\frac{di_{L}}{dt}\\ i_{C} &=& C\frac{dv_{C}}{dt} \end{eqnarray*}$

and the circuit connections dictate the relations

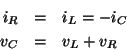
$\begin{eqnarray*}i_{R} &=& i_{L}=-i_{C}\\ v_{C} &=& v_{L}+v_{R} \end{eqnarray*}$

Combining these equations shows that the state of the circuit (summarized by v_C, the voltage across the capacitor, and i_L, the current in the inductor) is described by the pair of differential equations

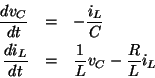
$\begin{eqnarray*}\frac{dv_{C}}{dt} &=& -\frac{i_{L}}{C}\\ \frac {di_{L}}{dt} &=& \frac{1}{L}v_{C}-\frac{R}{L}i_{L} \end{eqnarray*}$

The signal-flow diagram representing this system of differential equations is shown in figure .

$\begin{figure}\par\figcaption {A series RLC circuit.}\end{figure}$

$\begin{figure}\par\figcaption {A signal-flow diagram for the solution to a series RLC circuit.}\end{figure}$

Write a procedure RLC that takes as arguments the parameters R, L, and C of the circuit and the time increment dt. In a manner similar to that of the RC procedure of exercise , RLC should produce a procedure that takes the initial values of the state variables, v_{C_<<14060>>0} and i_{L_<<14061>>0}, and produces a pair (using cons) of the streams of states v_C and i_L. Using RLC, generate the pair of streams that models the behavior of a series RLC circuit with R = 1 ohm, C= 0.2 farad, L = 1 henry, dt = 0.1 second, and initial values i_{L_<<14066>>0} = 0 amps and v_{C_<<14067>>0} = 10 volts.
Normal-order evaluation
The examples in this section illustrate how the explicit use of delay and force provides great programming flexibility, but the same examples also show how this can make our programs more complex. Our new integral procedure, for instance, gives us the power to model systems with loops, but we must now remember that integral should be called with a delayed integrand, and every procedure that uses integral must be aware of this. In effect, we have created two classes of procedures: ordinary procedures and procedures that take delayed arguments. In general, creating separate classes of procedures forces us to create separate classes of higher-order procedures as well.
One way to avoid the need for two different classes of procedures is to make all procedures take delayed arguments. We could adopt a model of evaluation in which all arguments to procedures are automatically delayed and arguments are forced only when they are actually needed (for example, when they are required by a primitive operation). This would transform our language to use normal-order evaluation, which we first described when we introduced the substitution model for evaluation in section . Converting to normal-order evaluation provides a uniform and elegant way to simplify the use of delayed evaluation, and this would be a natural strategy to adopt if we were concerned only with stream processing. In section , after we have studied the evaluator, we will see how to transform our language in just this way. Unfortunately, including delays in procedure calls wreaks havoc with our ability to design programs that depend on the order of events, such as programs that use assignment, mutate data, or perform input or output. Even the single delay in cons-stream can cause great confusion, as illustrated by exercises and . As far as anyone knows, mutability and delayed evaluation do not mix well in programming languages, and devising ways to deal with both of these at once is an active area of research.

Previous: Exploiting the Stream Paradigm

Next: Modularity of Functional Programs and Modularity of Objects

webmaster@arsdigita.org