One way to view data abstraction is as an application of the
``principle of least commitment.'' In implementing the complex-number
system in section ![[*]](../image/cross_ref_motif.gif) , we can
use either Ben's rectangular representation or Alyssa's polar
representation. The abstraction barrier formed by the selectors and
constructors permits us to defer to the last possible moment the
choice of a concrete representation for our data objects and thus
retain maximum flexibility in our system design.
, we can
use either Ben's rectangular representation or Alyssa's polar
representation. The abstraction barrier formed by the selectors and
constructors permits us to defer to the last possible moment the
choice of a concrete representation for our data objects and thus
retain maximum flexibility in our system design.
The principle of least commitment can be carried to even further extremes. If we desire, we can maintain the ambiguity of representation even after we have designed the selectors and constructors, and elect to use both Ben's representation and Alyssa's representation. If both representations are included in a single system, however, we will need some way to distinguish data in polar form from data in rectangular form. Otherwise, if we were asked, for instance, to find the magnitude of the pair (3,4), we wouldn't know whether to answer 5 (interpreting the number in rectangular form) or 3 (interpreting the number in polar form). A straightforward way to accomplish this distinction is to include a type tag--the symbol rectangular or polar--as part of each complex number. Then when we need to manipulate a complex number we can use the tag to decide which selector to apply.
In order to manipulate tagged data, we will assume that we have procedures type-tag and contents that extract from a data object the tag and the actual contents (the polar or rectangular coordinates, in the case of a complex number). We will also postulate a procedure attach-tag that takes a tag and contents and produces a tagged data object. A straightforward way to implement this is to use ordinary list structure:
(define (attach-tag type-tag contents)
(cons type-tag contents))
(define (type-tag datum)
(if (pair? datum)
(car datum)
(error "Bad tagged datum - TYPE-TAG" datum)))
(define (contents datum)
(if (pair? datum)
(cdr datum)
(error "Bad tagged datum - CONTENTS" datum)))
Using these procedures, we can define predicates rectangular? and polar?, which recognize polar and rectangular numbers, respectively:
(define (rectangular? z) (eq? (type-tag z) 'rectangular)) (define (polar? z) (eq? (type-tag z) 'polar))
With type tags, Ben and Alyssa can now modify their code so that
their two different representations can coexist in the same system.
Whenever Ben constructs a complex number, he tags it as rectangular.
Whenever Alyssa constructs a complex number, she tags it as polar.
In addition, Ben and Alyssa must make sure that the names of their
procedures do not conflict. One way to do this is for Ben to append
the suffix rectangular to the name of each of his representation
procedures and for Alyssa to append polar to the names of hers.
Here is Ben's revised rectangular representation from
section ![[*]](../image/cross_ref_motif.gif) :
:
(define (real-part-rectangular z) (car z))
(define (imag-part-rectangular z) (cdr z))
(define (magnitude-rectangular z)
(sqrt (+ (square (real-part-rectangular z))
(square (imag-part-rectangular z)))))
(define (angle-rectangular z)
(atan (imag-part-rectangular z)
(real-part-rectangular z)))
(define (make-from-real-imag-rectangular x y)
(attach-tag 'rectangular (cons x y)))
(define (make-from-mag-ang-rectangular r a)
(attach-tag 'rectangular
(cons (* r (cos a)) (* r (sin a)))))
and here is Alyssa's revised polar representation:
(define (real-part-polar z)
(* (magnitude-polar z) (cos (angle-polar z))))
(define (imag-part-polar z)
(* (magnitude-polar z) (sin (angle-polar z))))
(define (magnitude-polar z) (car z))
(define (angle-polar z) (cdr z))
(define (make-from-real-imag-polar x y)
(attach-tag 'polar
(cons (sqrt (+ (square x) (square y)))
(atan y x))))
(define (make-from-mag-ang-polar r a)
(attach-tag 'polar (cons r a)))
Each generic selector is implemented as a procedure that checks the tag of its argument and calls the appropriate procedure for handling data of that type. For example, to obtain the real part of a complex number, real-part examines the tag to determine whether to use Ben's realpart-rectangular or Alyssa's real-part-polar. In either case, we use contents to extract the bare, untagged datum and send this to the rectangular or polar procedure as required:
(define (real-part z)
(cond ((rectangular? z)
(real-part-rectangular (contents z)))
((polar? z)
(real-part-polar (contents z)))
(else (error "Unknown type - REAL-PART" z))))
(define (imag-part z)
(cond ((rectangular? z)
(imag-part-rectangular (contents z)))
((polar? z)
(imag-part-polar (contents z)))
(else (error "Unknown type - IMAG-PART" z))))
(define (magnitude z)
(cond ((rectangular? z)
(magnitude-rectangular (contents z)))
((polar? z)
(magnitude-polar (contents z)))
(else (error "Unknown type - MAGNITUDE" z))))
(define (angle z)
(cond ((rectangular? z)
(angle-rectangular (contents z)))
((polar? z)
(angle-polar (contents z)))
(else (error "Unknown type - ANGLE" z))))
To implement the complex-number arithmetic operations, we can use the
same procedures add-complex, sub-complex,
mul-complex, and div-complex from
section ![[*]](../image/cross_ref_motif.gif) , because the
selectors they call are generic, and so will work with either
representation. For example, the procedure add-complex is still
, because the
selectors they call are generic, and so will work with either
representation. For example, the procedure add-complex is still
(define (add-complex z1 z2)
(make-from-real-imag (+ (real-part z1) (real-part z2))
(+ (imag-part z1) (imag-part z2))))
Finally, we must choose whether to construct complex numbers using Ben's representation or Alyssa's representation. One reasonable choice is to construct rectangular numbers whenever we have real and imaginary parts and to construct polar numbers whenever we have magnitudes and angles:
(define (make-from-real-imag x y) (make-from-real-imag-rectangular x y)) (define (make-from-mag-ang r a) (make-from-mag-ang-polar r a))
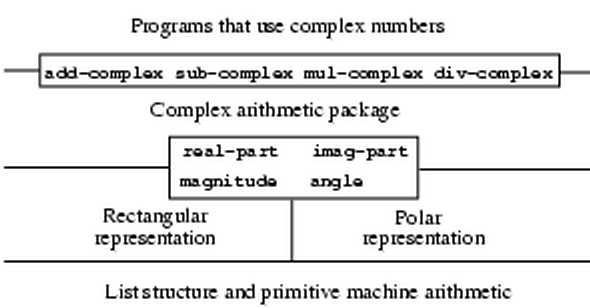
The resulting complex-number system has the structure shown in
figure ![[*]](../image/cross_ref_motif.gif) . The system has been
decomposed into three relatively independent parts: the
complex-number-arithmetic operations, Alyssa's polar
implementation, and Ben's rectangular implementation. The polar and
rectangular implementations could have been written by Ben and Alyssa
working separately, and both of these can be used as underlying
representations by a third programmer implementing the
complex-arithmetic procedures in terms of the abstract
constructor/selector interface.
. The system has been
decomposed into three relatively independent parts: the
complex-number-arithmetic operations, Alyssa's polar
implementation, and Ben's rectangular implementation. The polar and
rectangular implementations could have been written by Ben and Alyssa
working separately, and both of these can be used as underlying
representations by a third programmer implementing the
complex-arithmetic procedures in terms of the abstract
constructor/selector interface.
Since each data object is tagged with its type, the selectors operate
on the data in a generic manner. That is, each selector is defined to
have a behavior that depends upon the particular type of data it is
applied to. Notice the general mechanism for interfacing the separate
representations: Within a given representation implementation (say,
Alyssa's polar package) a complex number is an untyped pair
(magnitude, angle). When a generic selector operates on a number of
polar type, it strips off the tag and passes the contents on to
Alyssa's code. Conversely, when Alyssa constructs a number for general
use, she tags it with a type so that it can be appropriately
recognized by the higher-level procedures. This discipline of
stripping off and attaching tags as data objects are passed from level
to level can be an important organizational strategy, as we shall see
in section ![[*]](../image/cross_ref_motif.gif) .
.