In the previous examples we built representations for two kinds of compound data objects: rational numbers and algebraic expressions. In one of these examples we had the choice of simplifying (reducing) the expressions at either construction time or selection time, but other than that the choice of a representation for these structures in terms of lists was straightforward. When we turn to the representation of sets, the choice of a representation is not so obvious. Indeed, there are a number of possible representations, and they differ significantly from one another in several ways.
Informally, a set is simply a collection of distinct objects. To give
a more precise definition we can employ the method of data
abstraction. That is, we define ``set'' by specifying the operations
that are to be used on sets. These are union-set,
intersection-set, elementofset?, and adjoin-set.
Element-of-set? is a predicate that determines whether a given
element is a member of a set.
Adjoin-set takes an object and a
set as arguments and returns a set that contains the elements of the
original set and also the adjoined element.
Union-set computes
the union of two sets, which is the set containing each element that
appears in either argument.
Intersection-set computes the
intersection of two sets, which is the set containing only elements
that appear in both arguments. From the viewpoint of data abstraction, we
are free to design any representation that implements these operations
in a way consistent with the interpretations given above.![[*]](../image/foot_motif.gif)
Sets as unordered lists
One way to represent a set is as a list of its elements in which no
element appears more than once. The empty set is represented by the
empty list. In this representation, element-of-set? is similar
to the procedure memq of section ![[*]](../image/cross_ref_motif.gif) . It uses equal?
instead of eq? so that the set elements need not be symbols:
. It uses equal?
instead of eq? so that the set elements need not be symbols:
(define (element-of-set? x set)
(cond ((null? set) false)
((equal? x (car set)) true)
(else (element-of-set? x (cdr set)))))
Using this, we can write adjoin-set. If the object to be adjoined
is already in the set, we just return the set. Otherwise, we use
cons to add the object to the list that represents the set:
(define (adjoin-set x set)
(if (element-of-set? x set)
set
(cons x set)))
For intersection-set we can use a recursive strategy. If we
know how to form the intersection of set2 and the cdr
of set1, we only need to decide whether to include
the car of set1 in this. But this depends on whether (car
set1) is also in set2. Here is the resulting procedure:
(define (intersection-set set1 set2)
(cond ((or (null? set1) (null? set2)) '())
((element-of-set? (car set1) set2)
(cons (car set1)
(intersection-set (cdr set1) set2)))
(else (intersection-set (cdr set1) set2))))
In designing a representation, one of the issues we should be
concerned with is efficiency. Consider the number of steps required by our set
operations. Since they all use element-of-set?, the speed
of this operation has a major impact on the efficiency of the set
implementation as a whole. Now, in order to check whether an object
is a member of a set, element-of-set? may have to scan the
entire set. (In the worst case, the object turns out not to be in the
set.) Hence, if the set has n elements, element-of-set?
might take up to n steps. Thus, the number of steps
required grows as ![]() .
The number of steps required by adjoin-set, which uses this operation,
also grows as
.
The number of steps required by adjoin-set, which uses this operation,
also grows as ![]() .
For intersection-set, which does an
element-of-set? check for each element of set1, the number of steps
required grows as the product of the sizes of the sets involved, or
.
For intersection-set, which does an
element-of-set? check for each element of set1, the number of steps
required grows as the product of the sizes of the sets involved, or
![]() for two sets of size n. The same will be true of
union-set.
for two sets of size n. The same will be true of
union-set.
Exercise. Implement the union-set operation for the unordered-list representation of sets.
Exercise.
We specified that a set would be represented as a list with no
duplicates. Now suppose we allow duplicates. For instance,
the set ![]() could be represented as the list (2 3 2 1 3 2
2). Design procedures element-of-set?, adjoin-set,
union-set, and intersection-set that operate on this
representation. How does the efficiency of each compare with the
corresponding procedure for the non-duplicate representation? Are
there applications for which you would use this representation in
preference to the non-duplicate one?
could be represented as the list (2 3 2 1 3 2
2). Design procedures element-of-set?, adjoin-set,
union-set, and intersection-set that operate on this
representation. How does the efficiency of each compare with the
corresponding procedure for the non-duplicate representation? Are
there applications for which you would use this representation in
preference to the non-duplicate one?
Sets as ordered lists
One way to speed up our set operations is to change the representation
so that the set elements are listed in increasing order. To do this,
we need some way to compare two objects so that we can say which is
bigger. For example, we could compare symbols lexicographically, or
we could agree on some method for assigning a unique number to an
object and then compare the elements by comparing the corresponding
numbers. To keep our discussion simple, we will consider only the
case where the set elements are numbers, so that we can compare
elements using > and <. We will represent a set of
numbers by listing its elements in increasing order. Whereas our
first representation above allowed us to represent the set
![]() by listing the elements in any order, our new
representation allows only the list (1 3 6 10).
by listing the elements in any order, our new
representation allows only the list (1 3 6 10).
One advantage of ordering shows up in element-of-set?: In checking for the presence of an item, we no longer have to scan the entire set. If we reach a set element that is larger than the item we are looking for, then we know that the item is not in the set:
(define (element-of-set? x set)
(cond ((null? set) false)
((= x (car set)) true)
((< x (car set)) false)
(else (element-of-set? x (cdr set)))))
How many steps does this save? In the worst case, the item we are
looking for may be the largest one in the set, so the number of steps
is the same as for the unordered representation. On the other hand,
if we search for items of many different sizes we can expect that
sometimes we will be able to stop searching at a point near the
beginning of the list and that other times we will still need to
examine most of the list. On the average we should expect to have to
examine about half of the items in the set. Thus, the average
number of steps required will be about n/2.
This is still
We obtain a more impressive speedup with intersection-set. In
the unordered representation this operation required
![]() steps, because we performed a complete scan of set2 for
each element of set1. But with the ordered representation, we
can use a more clever method. Begin by comparing the initial
elements, x1 and x2, of the two sets. If x1
equals x2, then that gives an element of the intersection, and
the rest of the intersection is the intersection of the cdrs of
the two sets. Suppose, however, that x1 is less than x2.
Since x2 is the smallest element in set2, we can
immediately conclude that x1 cannot appear anywhere in
set2 and hence is not in the intersection. Hence, the intersection
is equal to the intersection of set2 with the cdr of
set1. Similarly, if x2 is less than x1, then the
intersection is given by the intersection of set1 with the
cdr of set2. Here is the procedure:
steps, because we performed a complete scan of set2 for
each element of set1. But with the ordered representation, we
can use a more clever method. Begin by comparing the initial
elements, x1 and x2, of the two sets. If x1
equals x2, then that gives an element of the intersection, and
the rest of the intersection is the intersection of the cdrs of
the two sets. Suppose, however, that x1 is less than x2.
Since x2 is the smallest element in set2, we can
immediately conclude that x1 cannot appear anywhere in
set2 and hence is not in the intersection. Hence, the intersection
is equal to the intersection of set2 with the cdr of
set1. Similarly, if x2 is less than x1, then the
intersection is given by the intersection of set1 with the
cdr of set2. Here is the procedure:
(define (intersection-set set1 set2)
(if (or (null? set1) (null? set2))
'()
(let ((x1 (car set1)) (x2 (car set2)))
(cond ((= x1 x2)
(cons x1
(intersection-set (cdr set1)
(cdr set2))))
((< x1 x2)
(intersection-set (cdr set1) set2))
((< x2 x1)
(intersection-set set1 (cdr set2)))))))
To estimate the number of steps required by this process, observe that at each
step we reduce the intersection problem to computing intersections of
smaller sets--removing the first element from set1 or
set2 or both. Thus, the number of steps required is at most the sum
of the sizes of set1 and set2, rather than the product of
the sizes as with the unordered representation. This is Exercise. Give an implementation of adjoin-set using the ordered representation. By analogy with element-of-set? show how to take advantage of the ordering to produce a procedure that requires on the average about half as many steps as with the unordered representation.
Exercise.
Give a ![]() implementation of
union-set for sets
represented as ordered lists.
implementation of
union-set for sets
represented as ordered lists.
Sets as binary trees
We can do better than the ordered-list representation by arranging the
set elements in the form of a tree. Each node of the tree holds one
element of the set, called the ``entry'' at that node, and a link to
each of two other (possibly empty) nodes. The ``left'' link points to
elements smaller than the one at the node, and the ``right'' link to
elements greater than the one at the node.
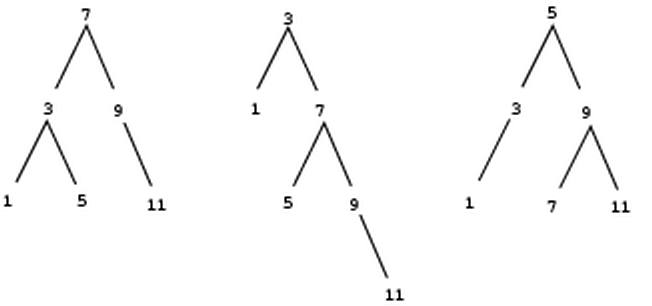
Figure ![[*]](../image/cross_ref_motif.gif) shows some trees that represent the set
shows some trees that represent the set
![]() .
The same set may be represented by a tree in a
number of different ways. The only thing we require for a valid
representation is that all elements in the left subtree be smaller
than the node entry and that all elements in the right subtree be
larger.
.
The same set may be represented by a tree in a
number of different ways. The only thing we require for a valid
representation is that all elements in the left subtree be smaller
than the node entry and that all elements in the right subtree be
larger.
The advantage of the tree representation is this: Suppose we want to
check whether a number x is contained in a set. We begin by
comparing x with the entry in the top node. If x is less than
this, we know that we need only search the left subtree; if x is
greater, we need only search the right subtree. Now, if the tree is
``balanced,'' each of these subtrees will be about half the size of
the original. Thus, in one step we have reduced the problem of
searching a tree of size n to searching a tree of size n/2. Since
the size of the tree is halved at each step, we should expect that the
number of steps needed to search a tree of size n grows as
![]() .
.![[*]](../image/foot_motif.gif) For large sets, this will
be a significant speedup over the previous representations.
For large sets, this will
be a significant speedup over the previous representations.
We can represent trees by using lists. Each node will be a list of
three items: the entry at the node, the left subtree, and the right
subtree. A left or a right subtree of the empty list will indicate
that there is no subtree connected there. We can describe this
representation by the following procedures:![[*]](../image/foot_motif.gif)
(define (entry tree) (car tree)) (define (left-branch tree) (cadr tree)) (define (right-branch tree) (caddr tree)) (define (make-tree entry left right) (list entry left right))
Now we can write the element-of-set? procedure using the strategy described above:
(define (element-of-set? x set)
(cond ((null? set) false)
((= x (entry set)) true)
((< x (entry set))
(element-of-set? x (left-branch set)))
((> x (entry set))
(element-of-set? x (right-branch set)))))
Adjoining an item to a set is implemented similarly and also requires
![]() steps. To adjoin an item x, we compare x with
the node entry to determine whether x should be added to the
right or to the left branch, and having adjoined x to the
appropriate branch we piece this newly constructed branch together
with the original entry and the other branch. If x is equal to
the entry, we just return the node. If we are asked to adjoin
x to an empty tree, we generate a tree that has x as the
entry and empty right and left branches. Here is the procedure:
steps. To adjoin an item x, we compare x with
the node entry to determine whether x should be added to the
right or to the left branch, and having adjoined x to the
appropriate branch we piece this newly constructed branch together
with the original entry and the other branch. If x is equal to
the entry, we just return the node. If we are asked to adjoin
x to an empty tree, we generate a tree that has x as the
entry and empty right and left branches. Here is the procedure:
(define (adjoin-set x set)
(cond ((null? set) (make-tree x '() '()))
((= x (entry set)) set)
((< x (entry set))
(make-tree (entry set)
(adjoin-set x (left-branch set))
(right-branch set)))
((> x (entry set))
(make-tree (entry set)
(left-branch set)
(adjoin-set x (right-branch set))))))
The above claim that searching the tree can be performed in a logarithmic
number of steps
rests on the assumption that the tree is
``balanced,'' i.e., that the
left and the right subtree of every tree have approximately the same
number of elements, so that each subtree contains about half the
elements of its parent. But how can we be certain that the trees we
construct will be balanced? Even if we start with a balanced tree,
adding elements with adjoin-set may produce an unbalanced
result. Since the position of a newly adjoined element depends on how
the element compares with the items already in the set, we can expect
that if we add elements ``randomly'' the tree will tend to be balanced
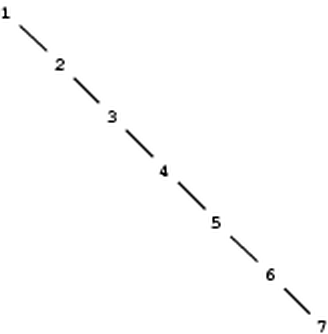
on the average. But this is not a guarantee. For example, if we
start with an empty set and adjoin the numbers 1 through 7 in sequence
we end up with the highly unbalanced tree shown in
figure ![[*]](../image/cross_ref_motif.gif) . In this tree all the left subtrees
are empty, so it has no advantage over a simple ordered list. One
way to solve this problem is to define an operation that transforms an
arbitrary tree into a balanced tree with the same elements. Then we
can perform this transformation after every few adjoin-set
operations to keep our set in balance. There are also other ways to
solve this problem, most of which involve designing new data
structures for which searching and insertion both can be done in
. In this tree all the left subtrees
are empty, so it has no advantage over a simple ordered list. One
way to solve this problem is to define an operation that transforms an
arbitrary tree into a balanced tree with the same elements. Then we
can perform this transformation after every few adjoin-set
operations to keep our set in balance. There are also other ways to
solve this problem, most of which involve designing new data
structures for which searching and insertion both can be done in
![]() steps.
steps.![[*]](../image/foot_motif.gif)
Exercise. Each of the following two procedures converts a binary tree to a list.
(define (tree->list-1 tree)
(if (null? tree)
'()
(append (tree->list-1 (left-branch tree))
(cons (entry tree)
(tree->list-1 (right-branch tree))))))
(define (tree->list-2 tree)
(define (copy-to-list tree result-list)
(if (null? tree)
result-list
(copy-to-list (left-branch tree)
(cons (entry tree)
(copy-to-list (right-branch tree)
result-list)))))
(copy-to-list tree '()))
a. Do the two procedures produce the same result for every tree? If
not, how do the results differ? What lists do the two procedures
produce for the trees in figure ![[*]](../image/cross_ref_motif.gif) ?
?
b. Do the two procedures have the same order of growth in the number
of steps required to convert a balanced tree with n elements to a list?
If not, which one grows more slowly?
Exercise. The following procedure list->tree converts an ordered list to a balanced binary tree. The helper procedure partial-tree takes as arguments an integer n and list of at least n elements and constructs a balanced tree containing the first n elements of the list. The result returned by partial-tree is a pair (formed with cons) whose car is the constructed tree and whose cdr is the list of elements not included in the tree.
(define (list->tree elements) (car (partial-tree elements (length elements))))(define (partial-tree elts n) (if (= n 0) (cons '() elts) (let ((left-size (quotient (- n 1) 2))) (let ((left-result (partial-tree elts left-size))) (let ((left-tree (car left-result)) (non-left-elts (cdr left-result)) (right-size (- n (+ left-size 1)))) (let ((this-entry (car non-left-elts)) (right-result (partial-tree (cdr non-left-elts) right-size))) (let ((right-tree (car right-result)) (remaining-elts (cdr right-result))) (cons (make-tree this-entry left-tree right-tree) remaining-elts))))))))
a. Write a short paragraph explaining as clearly as you can how
partial-tree works. Draw the tree produced by list->tree for
the list (1 3 5 7 9 11).
b. What is the order of growth in the number of steps required by
list->tree to convert a list of n elements?
Exercise.
Use the results of exercises ![[*]](../image/cross_ref_motif.gif) and
and
![[*]](../image/cross_ref_motif.gif) to give
to give ![]() implementations of
unionset and intersection-set for sets implemented as
(balanced) binary trees.
implementations of
unionset and intersection-set for sets implemented as
(balanced) binary trees.
![[*]](../image/foot_motif.gif)
Sets and information retrieval
We have examined options for using lists to represent sets and have seen how the choice of representation for a data object can have a large impact on the performance of the programs that use the data. Another reason for concentrating on sets is that the techniques discussed here appear again and again in applications involving information retrieval.
Consider a data base containing a large number of individual records, such as the personnel files for a company or the transactions in an accounting system. A typical data-management system spends a large amount of time accessing or modifying the data in the records and therefore requires an efficient method for accessing records. This is done by identifying a part of each record to serve as an identifying key. A key can be anything that uniquely identifies the record. For a personnel file, it might be an employee's ID number. For an accounting system, it might be a transaction number. Whatever the key is, when we define the record as a data structure we should include a key selector procedure that retrieves the key associated with a given record.
Now we represent the data base as a set of records. To locate the record with a given key we use a procedure lookup, which takes as arguments a key and a data base and which returns the record that has that key, or false if there is no such record. Lookup is implemented in almost the same way as element-of-set?. For example, if the set of records is implemented as an unordered list, we could use
(define (lookup given-key set-of-records)
(cond ((null? set-of-records) false)
((equal? given-key (key (car set-of-records)))
(car set-of-records))
(else (lookup given-key (cdr set-of-records)))))
Of course, there are better ways to represent large sets than as unordered lists. Information-retrieval systems in which records have to be ``randomly accessed'' are typically implemented by a tree-based method, such as the binary-tree representation discussed previously. In designing such a system the methodology of data abstraction can be a great help. The designer can create an initial implementation using a simple, straightforward representation such as unordered lists. This will be unsuitable for the eventual system, but it can be useful in providing a ``quick and dirty'' data base with which to test the rest of the system. Later on, the data representation can be modified to be more sophisticated. If the data base is accessed in terms of abstract selectors and constructors, this change in representation will not require any changes to the rest of the system.
Exercise. Implement the lookup procedure for the case where the set of records is structured as a binary tree, ordered by the numerical values of the keys.