Notes for Reading JCM ``A Dynamical Theory of the Electromagnetic Field''

Jerry Bolton, Jr.

Contents

• 1 Introduction
• 2 Notes and Errata
  • 2.1 Article (24) / 20010908
  • 2.2 Article (25) / 20010908
  • 2.3 Article (26) / 20010908
  • 2.4 Article (29) / 20010908
  • 2.5 Article (31) / 20020704

Abstract:

This is a collection of notes that is meant to supplement the JCM text. It contains additional mathetmatical and modeling notes which show how JCM arrived at various conclusions, and how some equations and solutions are derived or found mathematically.

1 Introduction

This paper provides supplemental information useful to readers of James Clerk Maxwell's ``A Dynamical Theory of the Electromagnetic Field.'' It contains diagrams and mathematical notes which show the steps for deriving JCM's solutions, which were omitted from his short paper. It also contains a number of alleged errata, prima rily textual, in the original JCM document. This paper is organized sequentially by JCM's original article number, and the author's notes are dated for each article.

2 Notes and Errata

2.1 Article (24) / 20010908

a body C connected to driving points A and B,with forces X and Y acting on these points.

The velocites of A,B, and C :

u = V_A

v = V_B

w = V_C

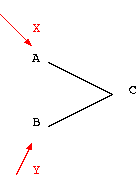
The velocity of C as a function of the velocities of A and B:

w = p ^. u + q ^. v

$${\frac{{d}}{{dt}}}$$w = p ^. $${\frac{{d}}{{dt}}}$$u + q ^. $${\frac{{d}}{{dt}}}$$v

The relation of the forces to the simultaneous displacement by the ``general equation of dynamics'':

C ^. $$\left(\vphantom{\frac{d}{dt}w\cdot\delta z}\right.$$$${\frac{{d}}{{dt}}}$$w ^. $$\delta$$z$$\left.\vphantom{\frac{d}{dt}w\cdot\delta z}\right)$$ = X ^. $$\delta$$x + Y ^. $$\delta$$y

The simultaneous displacement of C, A and B:

$$\delta$$z = p ^. $$\delta$$x + p ^. $$\delta$$y

Solving for X and Y, we have:

X = $${\frac{{\left(C\cdot\frac{d}{dt}w\cdot\delta z-Y\cdot\delta y\right)}}{{\delta x}}}$$

Y = $${\frac{{\left(C\cdot\frac{d}{dt}w\cdot\delta z-X\cdot\delta x\right)}}{{\delta y}}}$$

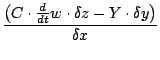
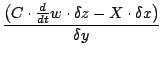
However, Maxwell has later need for equations without dependency on the simultaneous displacement. Therefore, we instead substitute for $\delta$z:

C ^. $${\frac{{d}}{{dt}}}$$w ^. $$\left(\vphantom{p\cdot\delta x+q\cdot\delta y}\right.$$p ^. $$\delta$$x + q ^. $$\delta$$y$$\left.\vphantom{p\cdot\delta x+q\cdot\delta y}\right)$$ = X ^. $$\delta$$x + Y ^. $$\delta$$y

Distributing we have:

C ^. $${\frac{{d}}{{dt}}}$$w ^. p ^. $$\delta$$x + C ^. $${\frac{{d}}{{dt}}}$$w ^. q ^. $$\delta$$y = X ^. $$\delta$$x + Y ^. $$\delta$$y

Maxwell concludes therefore¹ that:

C ^. $${\frac{{d}}{{dt}}}$$w ^. p = X

C ^. $${\frac{{d}}{{dt}}}$$w ^. q = Y

We substitute for ${\frac{{dw}}{{dt}}}$:

X = C ^. $$\left(\vphantom{p\cdot\frac{d}{dt}u+q\cdot\frac{d}{dt}v}\right.$$p ^. $${\frac{{d}}{{dt}}}$$u + q ^. $${\frac{{d}}{{dt}}}$$v$$\left.\vphantom{p\cdot\frac{d}{dt}u+q\cdot\frac{d}{dt}v}\right)$$ ^. p

Y = C ^. $$\left(\vphantom{p\cdot\frac{d}{dt}u+q\cdot\frac{d}{dt}v}\right.$$p ^. $${\frac{{d}}{{dt}}}$$u + q ^. $${\frac{{d}}{{dt}}}$$v$$\left.\vphantom{p\cdot\frac{d}{dt}u+q\cdot\frac{d}{dt}v}\right)$$ ^. q

Maxwell factors, distributes C and applies the sum rule of differentiation: (20010924)

X = $${\frac{{d}}{{dt}}}$$$$\left(\vphantom{C\cdot p^{2}\cdot u+C\cdot p\cdot q\cdot v}\right.$$C ^. p^{2 .} u + C ^. p ^. q ^. v$$\left.\vphantom{C\cdot p^{2}\cdot u+C\cdot p\cdot q\cdot v}\right)$$

Y = $${\frac{{d}}{{dt}}}$$$$\left(\vphantom{C\cdot p\cdot q\cdot u+C\cdot q^{2}\cdot v}\right.$$C ^. p ^. q ^. u + C ^. q^{2 .} v$$\left.\vphantom{C\cdot p\cdot q\cdot u+C\cdot q^{2}\cdot v}\right)$$

The momentum of C referred to A (as Maxwell calls it) is:

$$\rho_{{AC}}^{}$$ = C ^. p^{2 .} u + C ^. p ^. q ^. v

The momentum of B referred to A:

$$\rho_{{AB}}^{}$$ = C ^. p ^. q ^. u + C ^. q^{2 .} v

In a system of many such bodies:

L = $$\sum$$(Cp²)

M = $$\sum$$(Cpq)

N = $$\sum$$(Cq²)

The momentum of the system Ais therefore (Lu + Mv)and the momentum of Bis (Mu + Nv), therefore:

X = $${\frac{{d}}{{dt}}}$$(Lu + Mv)

Y = $${\frac{{d}}{{dt}}}$$(Mu + Nv)

2.2 Article (25) / 20010908

The force $\eta$ = ${\frac{{d}}{{dt}}}$Mufollows logically because u and v are independent. That is to say, the force $\eta$must change by this amount to stabilize Bwhen the velocity of Ais changed by ${\frac{{du}}{{dt}}}$.

2.3 Article (26) / 20010908

Maxwell points out that L, M, and Nare scalar functions of the form and relative position of the circuits. Are they not quaternion in nature? Why not?

2.4 Article (29) / 20010908

Maxwell states:

Sy + $${\frac{{d}}{{dt}}}$$(Mx + Ny) = 0

And also:

Y = $$\int_{{0}}^{{t}}$$ydt = $${\frac{{-Mx}}{{S}}}$$

We may reach this conclusion by the following manipulations:

Sy + $${\frac{{d}}{{dt}}}$$Mx + $${\frac{{d}}{{dt}}}$$Ny = 0

Sy + $${\frac{{d}}{{dt}}}$$Ny = - $${\frac{{d}}{{dt}}}$$Mx

y(S + $${\frac{{d}}{{dt}}}$$N) = - $${\frac{{d}}{{dt}}}$$Mx

y(S + 0) = - $${\frac{{d}}{{dt}}}$$Mx

y = - $${\frac{{d}}{{dt}}}$$$${\frac{{Mx}}{{S}}}$$

Therefore:

$$\int$$(y)dt = $$\int$$(- $${\frac{{d}}{{dt}}}$$$${\frac{{Mx}}{{S}}}$$)dt = - $${\frac{{M}}{{S}}}$$x

Which is precisely as Maxwell claims. Article (30) follows directly from this.

2.5 Article (31) / 20020704

Maxwell writes: ``multiply (1) by x and (2) by y, and add.'' He means: ``multiply (4) by x and (5) by y, and add.''

About this document ...

Notes for Reading JCM ``A Dynamical Theory of the Electromagnetic Field''

This document was generated using the LaTeX2HTML translator Version 2002-2 (1.70)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html -no_subdir -split 0 -show_section_numbers -no_math -html_version 3.2,math /home/jay/khazad/public_html/science/maxwell/maxwell.tex

The translation was initiated by Jay Bolton on 2004-05-23

Footnotes

... therefore¹

David Vomlehn comments (20010919) that this is a well-accepted shortcut and can be rigorously shown.